机器学习笔记：分类

分类问题与回归问题不同，是想要对输入数据给出一个类别的判断。想要实现这个目的，最直观的想法是可以用回归模型以给出的输出作为判断依据。例如对于二类分类问题，我们可以让模型输出一个位于$[-1,1]$的数字，让第一类数据以$1$作为label，让第二类数据以$-1$作为label。然后在预测时大于1则分为第一类，小于1则分为第二类。如下图所示：

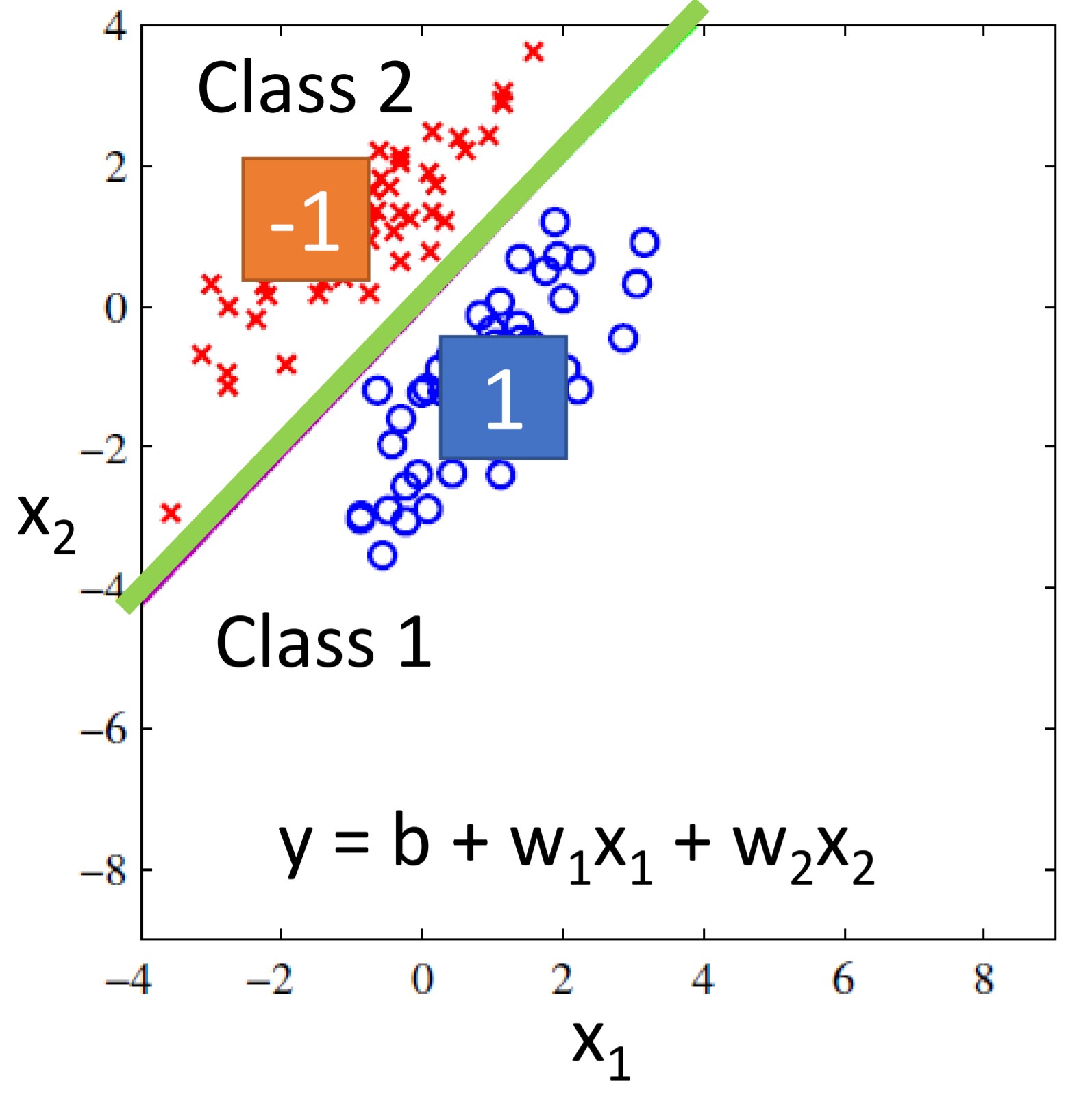
但这么做其实是有局限性的。因为当我们改变一下数据分布的样子，就会变成这样：

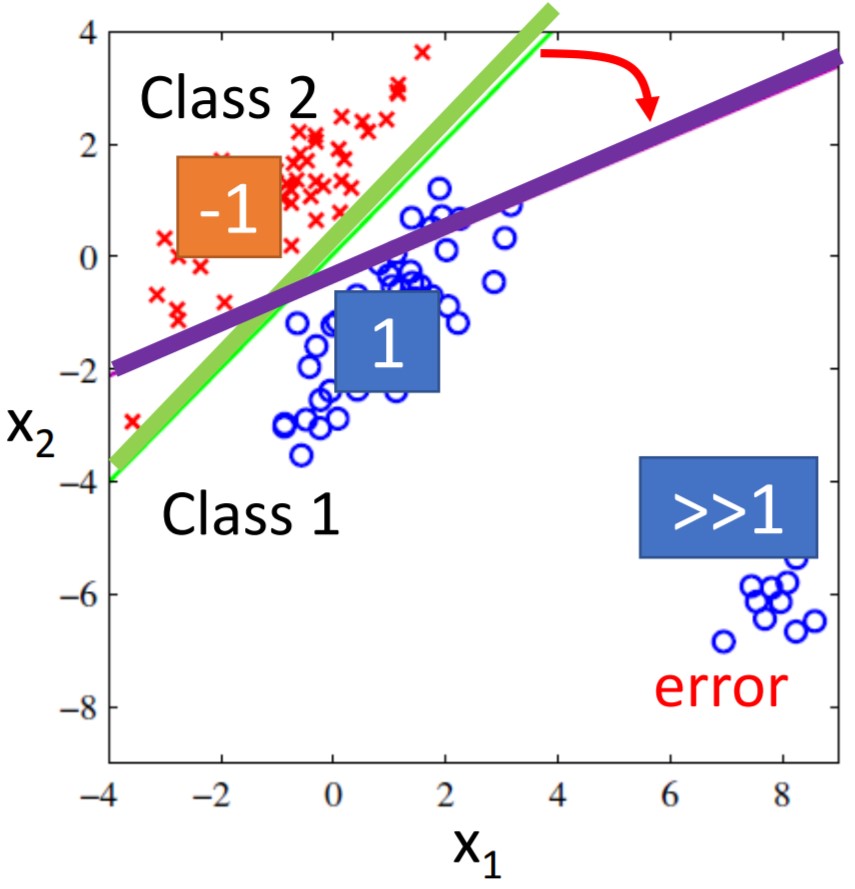
由于新的数据的加入，如果仍然用绿色线来作为判别分类，会导致右小角的那些新加入的样本的回归值远大于1。而模型为了避免这种情况的发生（想让所有蓝色点都尽量趋近于1），就会自发地将分类边界从绿色线向紫色线进行偏移。即如果考虑上图中所有数据点，学到的分了边界不会是绿色的线而是紫色的线。但显然对于分类任务来说，绿色应该是一个比较好的结果。这时候回归和分类会出现分期。

除此之外，回归模型也很难用在多类分类问题上。那么对于分类问题应该有一种专门的处理方式。

概率生成模型

例如我们可以设计一个模型$f(x)$，输入$x$，输入如果大于0则分类结果是第一类，否则是第二类。那我们该如何设计loss function？最直观的方式是“计数”。即“分类错误的次数”：

$$L(f)=\sum_n\delta(f(x^n)\neq\hat{y}^n)$$

对于优化这个函数，我们可以用梯度下降。然而，上面这个“计数”函数作为损失函数是没办法微分的，也就无法用梯度下降，所以需要先从理论的角度来分析一下分类问题。

加入现在有两个箱子：箱子1内有4个蓝球1个绿球。而箱子2内有两个蓝球3个绿球。我们规定有$2/3$的概率从箱子1中抽，有$1/3$的概率从箱子3中抽。即：

$$\begin{align} P(B_1)&=2/3 \\ P(B_2)&=1/3 \\ P(Blue|B_1) &= 4/5 \\ P(Green|B_1) &= 1/5 \\ P(Blue|B_1) &= 2/5 \\ P(Green|B_1) &= 3/5 \\ \end{align}$$

而现在我们抽到了一个蓝球，那么它是从两个盒子里抽出来的概率各是多少？即$P(B_1|Blue)=?$

利用贝叶斯公式可以得到：

$$P(B_1|Blue)=\frac{P(Blue|B_1)P(B_1)}{P(Blue|B_1)P(B_1) + P(Blue|B_2)P(B_2)}$$

此时如果把盒子1和盒子2换成类别1和类别2，则问题变成：“给定一个x，它从类别1和类别2中被生成出来的概率分别是多少”。这种模型就是“生成模型”。为什么要叫“生成模型”？因为只要我们有这个模型，就可以用模型来采样得到源源不断的x，即$P(x)=P(x|C_1)P(C_2)+P(x|C_2)P(C_2)$。

于是，我们现在的任务就变成了，给定一组同类数据的情况下，我们可以训练一个模型$p(x)$来作为这些数据被采样得到的概率。如果对于每一个类问题都有一个不同的模型，那么我们的任务就是对$p(x|C_x)$进行建模。

这里我们可以做出一个假设，即所有数据服从一个高斯分布。如下图：

$$f_{\mu,\Sigma}(x)=\frac{1}{(2\pi)^{D/2}}\frac{1}{|\Sigma|^{1/2}}\exp\left\{-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)\right\}$$

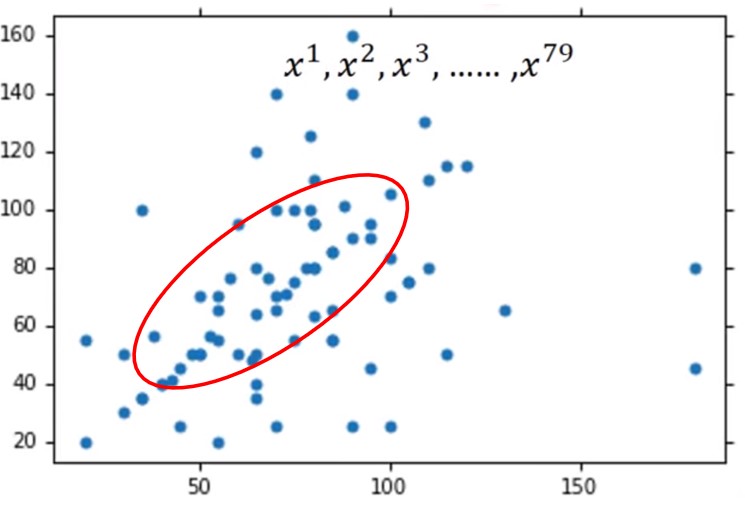
这个分布可以用来表示给定一个$x$是从这个分布中被采样得到的概率。而$\mu$和$\Sigma$则是这个模型的参数。那么现在的任务是寻找模型的这两个参数。那么该如何寻找？

这里所使用的方法就是给定一组训练数据，进行极大似然估计。任意一个数据从任意一个高斯分布中都有可能被采样得到，但他们采样得到的概率是不同的。而极大似然估计就是去寻找能够使得这组数据被采样得到的最有可能的那个高斯分布的参数：

$$L(\mu,\Sigma)=f_{\mu,\Sigma}(x^1)f_{\mu,\Sigma}(x^2)f_{\mu,\Sigma}(x^3)\dots f_{\mu,\Sigma}(x^N)$$

而我们的任务是去寻找其中使得上面这个似然函数$L$最大的那个$\mu^*$和$\Sigma^*$:

$$\mu^*,\Sigma^*=\arg\max_{\mu,\Sigma}L(\mu,\Sigma)$$

也就是通过穷举所有的$\mu$和$\Sigma$，找到能让$L(\mu,\Sigma)$最大的$\mu$和$\Sigma$。那么这个方程该如何解？一种直观的方法是对着公式直接解：

$$\begin{align} \mu^*&=\frac{1}{N}\sum_{i=1}^Nx^i \\ \Sigma^*&=\frac{1}{N}\sum_{i=1}^N(x^i-\mu^*)(x^i-\mu^*)^T \end{align}$$

对于不同的类别，都能算出各自类别的$\mu^*$和$\Sigma^*$，也就是说我们能够得到$P(x|C_1)$和$P(x|C_2)$。这两个分布就是分别由$(\mu^1, \Sigma^1)$和$(\mu^2, \Sigma^2)$决定的两个高斯分布。

然后在给定一个样本$x$时，它从第一类采样得到的概率为：

$$P(C_1|x)=\frac{P(x|C_1)P(C_1)}{P(x|C_1)P(C_1)+P(x|C_2)P(C_2)}$$

上式中的$P(C_1)$和$P(C_2)$可以直接通过计数得到（即统计分别属于$C_1$和$C_2$的样本的数量）。而$P(x|C_1)$和$P(x|C_2)$就是前面的结果。对于二类分类问题，当$P(C_1|x)>0.5$时即可以表示$x$属于$C_1$类，否则就是第二类。

线性模型

然而，这个模型其实并不是那么常用，因为由于不同的高斯分别用不同的协方差矩阵作$\Sigma$为参数，随着输入特征维度的增加，协方差矩阵内包含的参数也是平方级增长，所以很容易出现过拟合的情况。所以这就需要跟多的训练数据，或者使用下面这种简化的方法。

这种方法就是让两个高斯分布模型公用同一个协方差矩阵。此时对于二类分类问题我们可以重新放在一起，并用同一个似然函数（而不是对两类分别建模）来做极大似然估计：

$$L(\mu^1,\mu^2,\Sigma)=f_{\mu^1,\Sigma}(x^1)f_{\mu^1,\Sigma}(x^2)\dots f_{\mu^1,\Sigma}(x^{N_{C_1}})\times f_{\mu^2,\Sigma}(x^{N_{C_1}+1})f_{\mu^2,\Sigma}(x^{N_{C_1}+2})\dots f_{\mu^2,\Sigma}(x^{N_{C_1}+N_{C_2}})$$

其中$N_{C_1}$和$N_{C_2}$分别表示两类样本数量。此时计算$\mu^1$和$\mu^2$的方式和上面是一样的。而$\Sigma$则是由$\Sigma^1$和$\Sigma^2$的加权和组成：

$$\Sigma=\frac{N_{C_1}}{N_{C_1}+N_{C_2}}\Sigma^1+\frac{N_{C_2}}{N_{C_1}+N_{C_2}}\Sigma^2$$

如果我们把之前分别使用$\Sigma^1$和$\Sigma^2$的那个高斯模型的Decision Boundary画出来，是下面这样：

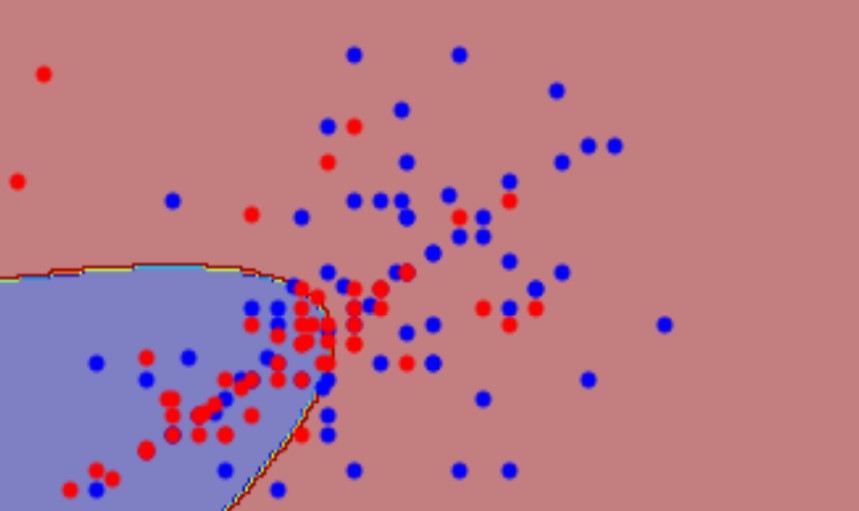
而当我们公用协方差矩阵$\Sigma$之后，这个Decision Boundary就会变成这样：

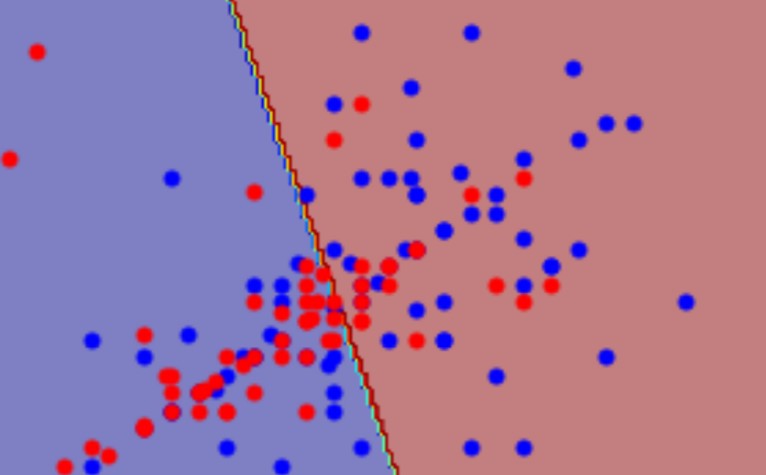
所以这个模型也被称为线性模型 (Linear Model)。尽管我们使用的是高斯模型，但这个模型由于Dicision Boundary是线性的，所以仍然叫做线性模型。而不共用协方差的模型也不叫作线性模型。

贝叶斯分类

我们再仔细研究一下所使用的概率模型。假设输入数据$\textbf{x}$是一个$K$维向量$[x_1,x_2,\dots,x_k,\dots,x_K]^T$，而且每一个维度之间是相互独立的，所以我们可以把$x$的概率$P(x)$拆解成各个维度之间概率的乘积：

$$P(\textbf{x}|C_1) = P(x_1|C_1)P(x_2|C_1)\dots P(x_k|C_1)\dots P(x_K|C_1)$$

然后我们再做一个额外的假设，即上面式子中每一个项$P(x_k|C_1)$都是一个一维高斯分布。此时我们完全忽略了输入特征各个维度之间的关系（相互独立），这个模型叫做朴素贝叶斯分类器 Naive Bayes Classifier。这个分类器的好处是效率比较高、模型简单、参数少、不容易过拟合。但这是建立在“特征的各个维度之间是相互独立的”这个假设之上的。如果数据不符合这个假设，这个方法也不会好。

除了Naive Bayes Classifier以外，从贝叶斯公式出发还能推导出其他的一些结论。我们将这贝叶斯公式的上下同除分子，并且进行一些推导：

$$P(C_1|x)=\frac{P(x|C_1)P(C_1)}{P(x|C_1)P(C_1)+P(x|C_2)P(C_2)}=\frac{1}{1+\frac{P(x|C_2)P(C_2)}{P(x|C_1)P(C_1)}} =\frac{1}{1+\exp(-z)}=\sigma(z)$$

其中$z=\log\frac{P(x|C_1)P(C_1)}{P(x|C_2)P(C_2)}$

上式其实就是Sigmoid函数。那么这个$z$究竟应该是什么样子？我们已知概率模型其实是$z$的一个Sigmoid函数：$P(C_1|x)=\sigma(z)$，此时我们对$z$进行进一步推导：

$$z=\log\frac{P(x|C_1)P(C_1)}{P(x|C_2)P(C_2)} = \log\frac{P(x|C_1)}{P(x|C_2)} + \log\frac{P(C_1)}{P(C_2)}$$

其中

$$\frac{P(C_1)}{P(C_2)}=\frac{\frac{N_{C_1}}{N_{C_1}+N_{C_2}}}{\frac{N_{C_2}}{N_{C_1}+N_{C2}}}=\frac{N_{C_1}}{N_{C_2}}$$

而我们知道$P(x|C_1)$和$P(x|C_2)$是两个高斯分布：

$$P(x|C_1)=\frac{1}{(2\pi)^{D/2}}\frac{1}{|\Sigma^1|^{1/2}}\exp\left\{-\frac{1}{2}(x-\mu^1)^T(\Sigma^1)^{-1}(x-\mu^1)\right\}$$ $$P(x|C_2)=\frac{1}{(2\pi)^{D/2}}\frac{1}{|\Sigma^2|^{1/2}}\exp\left\{-\frac{1}{2}(x-\mu^2)^T(\Sigma^2)^{-1}(x-\mu^2)\right\}$$

如果将上面两个式子相除再取对数，得：

$$\begin{align} \require{cancel} \log\frac{P(x|C_1)}{P(x|C_2)}&=\log\frac{\cancel{\frac{1}{(2\pi)^{D/2}}}\frac{1}{|\Sigma^1|^{1/2}}\exp\left\{-\frac{1}{2}(x-\mu^1)^T(\Sigma^1)^{-1}(x-\mu^1)\right\}}{\cancel{\frac{1}{(2\pi)^{D/2}}}\frac{1}{|\Sigma^2|^{1/2}}\exp\left\{-\frac{1}{2}(x-\mu^2)^T(\Sigma^2)^{-1}(x-\mu^2)\right\}} \\ &=\log\frac{|\Sigma^2|^{1/2}}{|\Sigma^1|^{1/2}}\exp\left\{-\frac{1}{2}\left[(x-\mu^1)^T(\Sigma^1)^{-1}(x-\mu^1)-(x-\mu^2)^T(\Sigma^2)^{-1}(x-\mu^2)\right]\right\} \\ &=\log\frac{|\Sigma^2|^{1/2}}{|\Sigma^1|^{1/2}}-\frac{1}{2}\left[(x-\mu^1)^T(\Sigma^1)^{-1}(x-\mu^1)-(x-\mu^2)^T(\Sigma^2)^{-1}(x-\mu^2)\right] \end{align}$$

对于上面得式子$(x-\mu^1)^T(\Sigma^1)^{-1}(x-\mu^1)$，展开得到：

$$\begin{align} (x-\mu^1)^T(\Sigma^1)^{-1}(x-\mu^1)&=x^T(\Sigma^1)^{-1}x-x^T(\Sigma^1)^{-1}\mu^1 -(\mu^1)^T(\Sigma^1)^{-1}x+(\mu^1)^T(\Sigma^1)^{-1}\mu^1 \\ &=x^T(\Sigma^1)^{-1}x-2(\mu^1)^T(\Sigma^1)^{-1}x+(\mu^1)^T(\Sigma^1)^{-1}\mu^1 \end{align}$$

对于$(x-\mu^2)^T(\Sigma^2)^{-1}(x-\mu^2)$展开也是同理：

$$(x-\mu^2)^T(\Sigma^2)^{-1}(x-\mu^2)=x^T(\Sigma^2)^{-1}x-2(\mu^2)^T(\Sigma^2)^{-1}x+(\mu^2)^T(\Sigma^2)^{-1}\mu^2$$

于是对于$z$：

$$\begin{align} z=&\log\frac{|\Sigma^2|^{1/2}}{|\Sigma^1|^{1/2}} - \frac{1}{2}x^T(\Sigma^1)^{-1}x+(\mu^1)^T(\Sigma^1)^{-1}x-\frac{1}{2}(\mu^1)^T(\Sigma^1)^{-1}\mu^1 \\\\ &+ \frac{1}{2}x^T(\Sigma^2)^{-1}x+(\mu^2)^T(\Sigma^2)^{-1}x+\frac{1}{2}(\mu^2)^T(\Sigma^2)^{-1}\mu^2+\log\frac{N_{C_1}}{N_{C_2}} \end{align}$$

由于我们之前假设过协方差矩阵可以公用，即：$\Sigma^1=\Sigma^2=\Sigma$，此时原来的$z$中有一些地方就可以化简：

$$\require{cancel} \begin{align} z =& \cancel{\log\frac{|\Sigma^2|^{1/2}}{|\Sigma^1|^{1/2}}} - \cancel{\frac{1}{2}x^T(\Sigma^1)^{-1}x} + (\mu^1)^T(\Sigma^1)^{-1}x-\frac{1}{2}(\mu^1)^T(\Sigma^1)^{-1}\mu^1 \\\\ &+ \cancel{\frac{1}{2}x^T(\Sigma^2)^{-1}x}+(\mu^2)^T(\Sigma^2)^{-1}x+\frac{1}{2}(\mu^2)^T(\Sigma^2)^{-1}\mu^2+\log\frac{N_{C_1}}{N_{C_2}} \\\\ =&(\mu^1-\mu^2)^T\Sigma^{-1}x-\frac{1}{2}(\mu^1)^T(\Sigma^1)^{-1}\mu^1+\frac{1}{2}(\mu^2)^T(\Sigma^2)^{-1}\mu^2+\log\frac{N_{C_1}}{N_{C_2}} \end{align}$$

此时如果假设$(\mu^1-\mu^2)^T\Sigma^{-1}x=\textbf{w}^T$，$\frac{1}{2}(\mu^1)^T(\Sigma^1)^{-1}\mu^1+\frac{1}{2}(\mu^2)^T(\Sigma^2)^{-1}\mu^2+\log\frac{N_{C_1}}{N_{C_2}}=b$，于是：

$$\begin{align} z&=w^Tx+b \\ P(C_1|x)&=\sigma(w\cdot x+b) \end{align}$$

也就是说，只要我们有数据，我们通过统计得到$N_{C_1},N_{C_2},\mu^1,\mu^2,\Sigma$，然后就可以计算得到$w$和$b$，从而得到模型$P(C_1|x)$。但其实仔细想想，前面那么复杂的一大堆东西，本身也就是一个参数，我们完全可以用梯度下降的方式直接寻找$w$和$b$。而这个过程其实就是Logistic Regression。也就是说，当出现可以公用的协方差矩阵的时候，利用了正态分布的模型其实和Logistic Regression本质上没有什么区别。或者说高斯模型也是Logistic Regression中的一种。只不过Logistic Regression没有假设模型的分布，而是通过利用梯度下降等方法学习到的参数决定了模型。但高斯模型假设数据本身服从高斯分布，它的参数可以直接从样本中通过统计量计算得到。

Logistic Regression

如果要仔细分析Logistic Regression背后的理论，还是从概率模型本身出发。

例如我们现在有一个分类模型$P_{w,b}(C_1|x)$，表示给定输入特征$x$时，它属于类别$C_1$的概率。如果 $P_{w,b}(C_1|x)>0.5$就说这个样本是属于类别$C_1$的，反之就是属于$C_2$的。对于Logistic Regression来说，模型可以是$P_{w,b}(C_1|x)=\sigma(z)$，其中$z=w\cdot x+b=\sum_iw_ix_i+b$。所以现在“函数集”可以表示成：

$$f_{w,b}(x)=P_{w,b}(C_1|x)$$

其中$w,b$是作为参数，通过改变取值，就可以遍历整个函数空间。接下来我们需要一种方式来评价不同的$w,b$决定的$f_{w,b}$的好坏。

假设我们现在有一组由N个样本组成的训练数据，分别属于两个类别：$\left\{(x^1,C_1), (x^2,C_1), (x^3,C_2), \dots, (x^N,C_1)\right\}$。假设这些训练数据是从$f_{w,b}(x)=P_{w,b}(C_1|x)$这个后验概率分布产生的。所以这个寻找“最佳函数”的操作就变成了：我们要寻找一组参数$w^*$和$b^*$，使得使用了这组参数的模型$f_{w,b}(x)$产生这组训练数据的概率最大，也就是极大似然估计：

$$L(w,b)=f_{w,b}(x^1)\cdot f_{w,b}(x^2)\cdot\left(1 - f_{w,b}(x^3)\right)\dots f_{w,b}(x^N) \\\\ w^*,b^*=\arg\max_{w,b}L(w,b)$$

这个式子中已经融入了样本类别，对于$C_1$来说，就是函数值本身，对于$C_2$来说，则是$1-f_{w,b}(x)$。然后对上面的公式取ln之后加上负号，把最大化变成最小化。这个操作不会改变找到的$w^*$和$b^*$：

$$w^*,b^*=\arg\max_{w,b}L(w,b)=\arg\min_{w,b}-\log L(w,b)$$

整理一下这个公式，由于取了对数，所以可以连乘表示的$L(w,b)$拆解成连加：

$$-\log L(w,b) = -\log f_{w,b}(x^1) - \log f_{w,b}(x^2) - \log (1-f_w,b(x3)) \dots$$

然而这样做有一个缺点就是属于不同类别的因式项的样子不一样，我们可以将它们换一个形式并最终用连加的记号表示（省略了$f_{w,b}$中的参数）：

$$\begin{align} \require{cancel} -\log L(w,b) =& \\ \cancel{-\log f(x^1)} &\rightarrow -\left[\hat{y}^1\log f(x^1)+(1-\hat{y}^1)\log(1-f(x^1))\right] \\ \cancel{-\log f(x^2)} &\rightarrow -\left[\hat{y}^2\log f(x^2)+(1-\hat{y}^2)\log(1-f(x^2))\right] \\ \cancel{-\log (1-f(x^3))} &\rightarrow -\left[\hat{y}^3\log f(x^3)+(1-\hat{y}^3)\log(1-f(x^3))\right] \\ &\dots \\ =&\sum_n-\left[\hat{y}^n\log f_{w,b}(x^n)+(1-\hat{y}^n)\log\left(1-f_{w,b}(x^n)\right)\right] \end{align}$$

上面中括号内部的内容叫做Cross-Entropy，因为这其实是两个伯努利分布的Cross-Entropy（尽管上面推导过程并没有体现信息论的知识，不过殊途同归）。假设有一个分布$p$:

$$\begin{align} p(x=1)&=\hat{y}^n \\ p(x=0)&=1 - \hat{y}^n \end{align}$$

和一个分布$q$:

$$\begin{align} q(x=1)&=f(x^n) \\ q(x=0)&=1-f(x^n) \end{align}$$

计算这两个分布的Cross-Entropy($H(p,q)=-\sum_xp(x)\log(q(x))$)就会得到上面中括号里的内容。

在得到这个损失函数之后，我们直接用Gradient Descent来优化。即对$-\log L(w,b)$计算$\partial w_i$。想要计算它的偏微分，需要先计算$\log f_{w,b}(x^n)$和$\log(1-f_{w,b}(x^n))$分别对$w_i$的偏微分。

已知

$$\begin{align} f_{w,b}(x)&=\sigma(z)=\frac{1}{1+\exp(-z)} \\ z&=\textbf{w}\cdot \textbf{x}+b=\sum_iw_ix_i+b \end{align}$$

首先我们计算第一项偏微分：

$$\begin{align} \frac{\partial\log f_{w,b}(x)}{\partial w_i}=\frac{\partial\log f_{w,b}(x)}{\partial z}\frac{\partial z}{\partial w_i} \end{align}$$

其中$\frac{\partial z}{\partial w_i}=x_i$，而

$$\require{cancel} \frac{\partial\log f_{w,b}(x)}{\partial z}=\frac{\partial\log\sigma(z)}{\partial z}=\frac{1}{\sigma(z)}\frac{\partial \sigma(z)}{\partial z}=\frac{1}{\cancel{\sigma(z)}}\cancel{\sigma(z)}(1-\sigma(z))=1-f_{w,b}(x)$$

所以

$$\frac{\partial\log f_{w,b}(x)}{\partial w_i}=(1-f_{w,b}(x))x_i$$

而上面求和里的第二项的偏导数也是类似：

$$\require{cancel} \begin{align} \frac{\partial\log(1-f_{w,b}(x))}{\partial w_i} \\ &=\frac{\partial\log(1-f_{w,b}(x))}{\partial z}\frac{\partial z}{\partial w_i}=\frac{\partial\log(1-\sigma(z))}{\partial z}x_i \\ &=-\frac{1}{1-\sigma(z)}\frac{\partial\sigma(z)}{\partial z}x_i \\ &=-\frac{1}{\cancel{1-\sigma(z)}}\sigma(z)\cancel{(1-\sigma(z))}x_i\\ &=-\sigma(z)x_i=-f_{w,b}(x)x_i \end{align}$$

所以回到损失函数

$$\begin{align} -\log L(w,b) = \sum_n-\left[\hat{y}^n\log f_{w,b}(x^n)+(1-\hat{y}^n)\log\left(1-f_{w,b}(x^n)\right)\right] \end{align}$$

对$w$求导则有

$$\require{cancel} \begin{align} \frac{\partial-\log L(w,b)}{\partial w} &=\sum_n-\left[\hat{y}^n(1-f_{w,b}(x^n))x_i^n-(1-\hat{y}^n)f_{w,b}(x^n)x_i^n\right] \\ &=\sum_n-\left[\hat{y}^n-\cancel{\hat{y}^nf_{w,b}(x^n)}-f_{w,b}(x^n)+\cancel{\hat{y}^nf_{w,b}(x^n)}\right]x_i^n \\ &=\sum_n-\left(\hat{y}^n-f_{w,b}(x^n)\right)x_i^n \end{align}$$

于是，利用梯度下降法对参数$w_i$进行更新的公式就是：

$$w_i\leftarrow w_i-\eta\sum_n-\left(\hat{y}-f_{w,b}(x^n)\right)x_i^n$$

神奇的是，回顾一下Linear Regression，在使用均方误差时所使用的更新公式和上面这个式子是一模一样的。唯一的区别是，在做Logistic Regression时，数据集中的$\hat{y}$都是非零即一的，而做Linear Regression时，$\hat{y}$值可以是任意实数。

那么这时候就有一个问题了：能不能把Linear Regression中的均方误差用在Logistic Regression中？

MSE x LR

如果在Logistic Regression中使用MSE作为损失函数会怎么样？即对函数

$f_{w,b}(x)=\sigma\left(\sum_iw_ix_i+b\right)$

用MSE构造损失函数：

$$L(f)=\frac{1}{2}\sum_n\left(f_{w,b}(x^n)-\hat{y}^n\right)^2$$

此时求偏微分：

$$\begin{align} \frac{\partial(f_{w,b}(x)-\hat{y})^2}{\partial w_i} &=\frac{\partial(\sigma(z)-\hat{y})}{\partial w_i}\\ &=2(\sigma(z)-\hat{y})\frac{\partial\sigma(z)}{\partial z}\frac{\partial z}{\partial w_i} \\ &=2(\sigma(z)-\hat{y})\sigma(z)\left(1-\sigma(z)\right)x_i \\ &=2(f_{w,b}(x)-\hat{y})f_{w,b}(x)\left(1-f_{w,b}(x)\right)x_i \end{align}$$

此时会有什么问题？由于$f_{w,b}(x)$这一项的存在，当模型输出在0附近时，无论$\hat{y}$是多少，它的偏微分仍然是一个很接近零的很小的数字，这会让下降速度非常慢。同样地，由于$1-f_{w,b}(x)$这一项的存在，当模型输出在1附近时，它的偏微分同样是一个比较小的数字。这个现象可以从下面这张图中看出来：

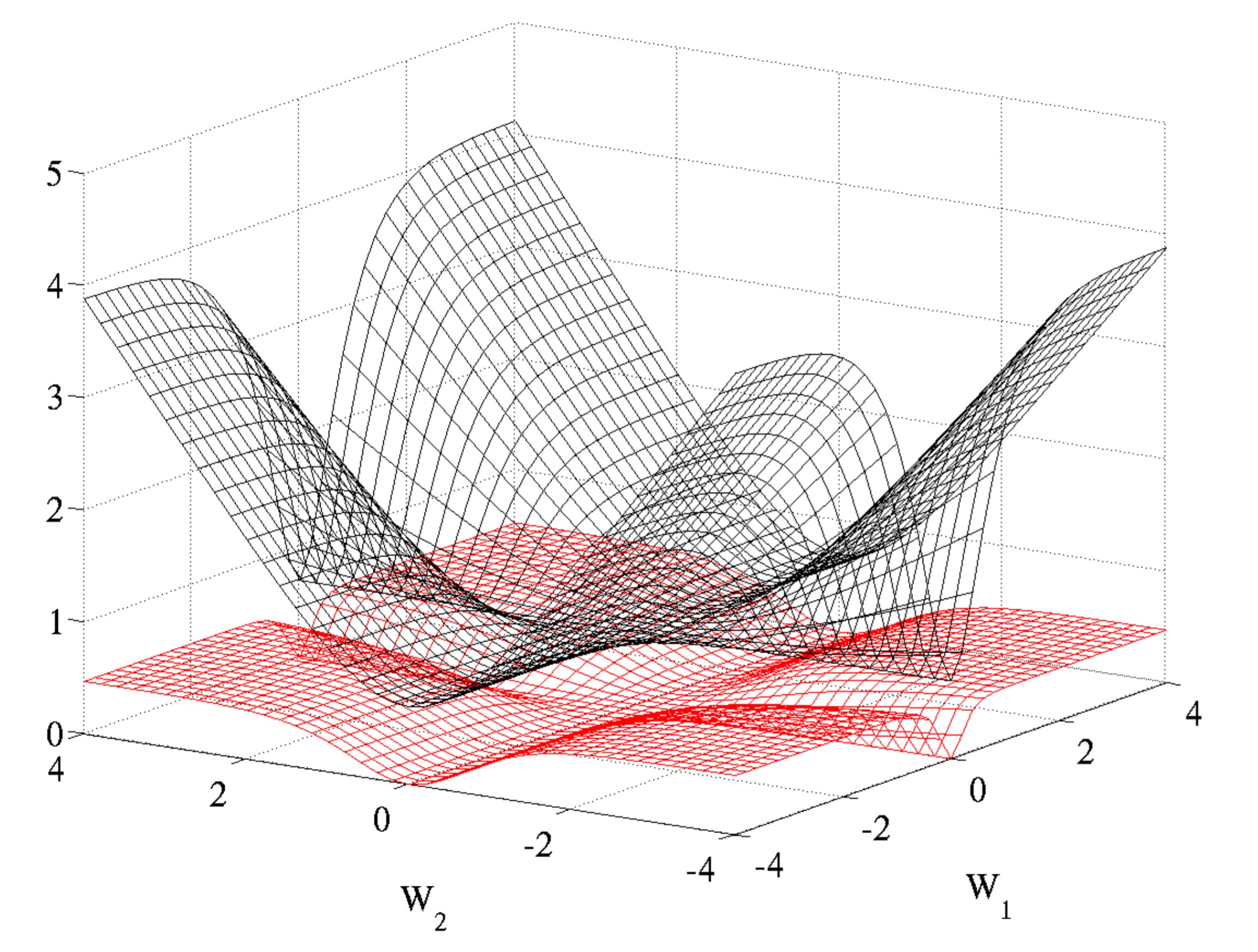(source:http://proceedings.mlr.press/v9/glorot10a/glorot10a.pdf)

上图中黑色的网格使用了交叉熵，红色的网格使用了MSE。这意味着当距离目标很远的时候，使用MSE会导致梯度比较小，变得非常难以训练。

生成模型与判别模型

我们称Logistic Regression为判别模型(Discriminative Model)，而称之前通过假设的高斯模型分别对每一类进行建模的方法为生成模型(Generative Model)。但实际上，这两个模型的是一样的（其中生成模型是共用协方差矩阵的情况）：

$$P(C_1|x)=\sigma(w\cdot x+b)$$

此时对于判别模型来说可以通过梯度下降之类的方法找到$w$和$b$。而对于生成模型来说，$w$和$b$是通过计算得到的：

$$\begin{align} w^T&=(\mu^1-\mu^2)^T\Sigma^{-1} \\ b&=-\frac{1}{2}(\mu^1)^T\Sigma^{-1}\mu^1+\frac{1}{2}(\mu^2)^T\Sigma^{-1}\mu^2+\log\frac{N_{C_1}}{N_{C_2}} \end{align}$$

那么现在问题来了，如果我们比较Discriminative Model和Generative Model所找到的最佳的$w$和$b$，他们会是一样的吗？答案是不会。即便两种方法用了同样的模型，从同样的函数空间取挑选模型，但是由于我们对两种model做了不同的假设，所以找到的参数是不同的。对于判别模型，我们没有做任何限制，直接从随机初始化的$w$和$b$出发开始用梯度下降法进行寻找。而对于生成模型，我们首先假设了一个数据生成分布，例如高斯分布。然后以高斯模型的角度出发来寻找$w$和$b$。

那么既然两种方法找到的参数不一样，那究竟那种方法找到的参数更好？这个因任务和数据情况而异。下面举一个例子。假设现在有一组训练数据，每一个数据的特征是二维向量，并且分别属于两个类别。其中包括1个$[(1,1), C_1]$，4个$[(1,0), C_2]$，4个$[(0,1), C_2]$和4个$[(0,0), C_2]$共计13条数据。此时如果给出一个未标注数据$[(1,1)]$，根据我们的直觉它应该属于$C_1$类别而不是$C_2$类别。

那么对于属于生成模型的朴素贝叶斯分类器来说，我们假设了特征的每一个维度之间是相互独立的，即$P(x|C_i)=P(x_1|C_i)P(x_2|C_i)$。此时我们能够从训练数据中知道以下信息：

$$\begin{align} P(C_1)&=\frac{1}{13} \\ P(C_2)&=\frac{12}{13} \\ P(x_1=1|C_1)&=1 \\ P(x_2=1|C_1)&=1 \\ P(x_1=1|C_2)&=\frac{1}{3} \\ P(x_2=1|C_2)&=\frac{1}{3} \end{align}$$

此时我们计算$P(C_1|x)$给定$x=[(1,1)]$时的概率：

$$P(C_1|x)=\frac{P(x|C_1)P(C_1)}{P(x|C_1)P(C_1)+P{x|C_2}P(C_2)}\approx0.429$$

我们会发现此时朴素贝叶斯分类器会倾向于让这个样本被分类成$C_2$类别。这是由于对于朴素贝叶斯模型来说，特征的两个维度是相互独立的。由于$C_2$样本中曾经分别出现过两个维度等于1的样本，所以输入的$[(1,1)]$也是有可能被模型生成出来的，只是采样的数据不够多而已。如果采样数据够多，是有可能采样出$[(1,1),C_2]$这样的样本的。于是朴素贝叶斯通过这种假设来做出了这种“反直觉”的结论。这种结论有时候会损害性能，但有时候反而是有优势的，例如：

1. 判别模型的性能会随着训练数据量影响较大。数据比较多时性能越来越好，但如果数据不够多，就不能起到足够的判别作用。此时生成模型通过假设变相地融入了人对数据特征的理解，从而减少多数据量的需求。生成模型一些时候会遵从假设，而并不太关注于数据本身。
2. 除此之外，如果数据的label本身就带有噪声，而生成模型所做出的假设可能会忽视这些噪声。
3. 在使用判别模型时，我们是直接对后验概率进行建模。而对于生成模型，我们会将模型(如$P(C_1|x)$)拆成先验概率(如$P(C_1)$)和类别相关的概率(如$P(x|C_1)$和$P(x|C_2)$，每一类都有各自的模型)的两部分来计算。这样的好处是这些部分可以单独进行训练。例如语音识别中的语言模型可以只用语言来单独进行训练。