线性回归

回归通常是指在给定一个输入之后，模型给出一个数值作为输出。例如股票预测在输入之前的走势后给出对当天股价的预测。

典型的回归模型通常包括下面几个部分

模型

对于一个特定任务来说，存在一个包含了大量函数的function set。这些函数就是处理这个任务的模型。例如

$$y=\textbf{w}\cdot \textbf{x} + b$$

就是一个线性模型。

函数的“好坏”

当我们有一系列训练数据之后，我们就要定义如何判断一个模型$f$的“好坏”。这个评价函数的函数就是损失函数：输入一个函数（函数内部由参数决定），输出这个输入的函数有多“差”。例如可以用下面这个函数作为损失函数：

$$L(f)=L(w,b)=\sum_{i=1}^{K}\left(\hat{y}_i - (w\cdot x_{i} + b)\right)^2$$

通过调整模型$f$的参数$w$和$b$，相当于从函数集合中“挑选”不同的模型。而我们的目的是想要挑出最好的函数$f^*$，即：

$$f^* = \arg\min_{f}L(f) = \arg\min_{w,b}\sum_{i=1}^K(\hat{y}_i - (w\cdot x_i + b))^2$$

即“在函数集合中遍历$f$，并挑出其中使损失函数最小的那个$f^*$”。

优化损失函数：梯度下降

现在问题变成，如何寻找让损失函数达到最小的参数$w$（$b$同理，下略），即：

$$w^* = \arg\min_wL(w)$$

此时就可以使用“梯度下降”的方法来进行这个任务。首先随即初始化一个值作为$w$的起始位置$w^0$。然后计算当$w=w^0$时$L$的梯度，即：

$$\frac{dL}{dw}\Bigr|_{\substack{w=w^0}}$$

此时，如果导数斜率是负数，则$w$应该增加，应该减小。那么增大或者减小的这个值则是：

$$w_1 \leftarrow w_0 - \eta\frac{dL}{dw}\Bigr|_{\substack{w=w^0}}$$

然后继续进行同样的操作：

$$w_2 \leftarrow w_0 - \eta\frac{dL}{dw}\Bigr|_{\substack{w=w^1}}$$

反复进行这个步骤，最终损失函数会达到收敛的状态。（Linear Model没有Local minimal）。继续推导这个偏微分（因为分别包含$w$和$b$两个参数）:

$$L(w,b)=\sum_{i=1}^K(\hat{y}_i - (b + w\cdot x_i))^2$$ $$\frac{\partial L}{\partial w}=\sum_{i=1}^K2(\hat{y}_i - (b + w\cdot x_i))(-x_i)$$ $$\frac{\partial L}{\partial b}=\sum_{i=1}^K2(\hat{y}_i - (b + w\cdot x_i))(-1)$$

经过训练我们会发现，这个一阶的模型并不一定能提供一个最好（使$L=0$）的结果。我们可以通过增加输入数据的次数，例如

$$y_i=b + w_1\cdot x_i + w_2\cdot (x_i)^2 + w_3\cdot (x_3)^2\cdots$$

这些不同的模型设计，会对模型能够达到的损失函数有不同的影响。通常来说，模型的次数越高，能够让模型在训练集上的损失越小。这个现象也是很合理的。

上图中表示了五种不同阶数的模型。右上角的表格表示在训练集上各个模型能够达到的最低损失。右下角的椭圆表示每一个模型所能表示的函数空间：低阶模型表示能力弱，而高阶模型能表达更大范围的函数。其实这个现象很自然，因为当高阶模型最高阶权重为0时就等于次阶模型。

然而当在测试集上的曲线则不一样：

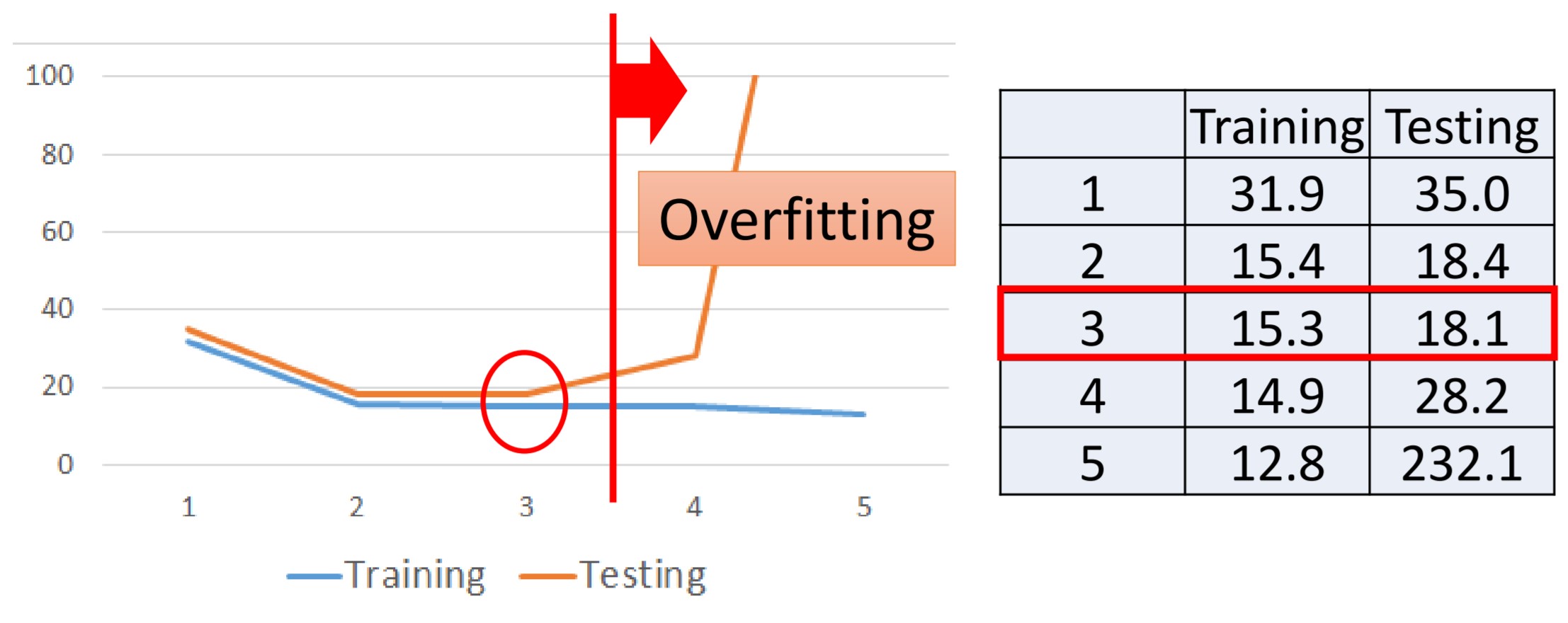
上图中，随着阶数提高，训练集损失越来越低但测试集上损失反而会出现增长。这个现象叫做overfitting（如上图红色竖线向右的方向就是越来越严重的overfitting）。所以我们需要人为选择一个比较好的模型。

正则化

在发生过拟合之后，除了降低模型复杂度以外，还可以通过增加一个正则项来环节。即在损失函数后面增加一项：

$$L=\sum_n(\hat{y}^n-(b + \sum w_ix_i))^2 + \lambda\sum(w_i)^2$$

后面的正则项能够对学习到的参数进行“平滑”，防止参数过大。为什么我们认为“不要过大”的参数是“好”参数呢？当我们对输入$x_i$做一个微小的变化$\Delta x_i$时，对应的输出$y$也会产生一个变化$w_i\Delta x_i$。可见，当$w_i$比较小的时候，$y$的变化也会不太敏感。为什么这种平滑会比较好？一个解释是，经过平滑之后，模型对输入数据中的噪声（即$\Delta x_i$）变得不会太敏感。

误差分析

上一节中提到的线性模型，随着模型复杂程度的提高，模型训练收敛之后在测试集上的性能反而可能变差。这些Error主要来源于两类：

1. Bias 偏差
2. Variance 方差

研究Error的来源非常重要，这使得我们能够有的放矢地改进模型。所以下面我们研究一下误差背后的细节。

假设存在一个“真实模型”：

$$\hat{y}=\hat{f}(x)$$

但我们并不直接知道真实模型$\hat{f}$本身，而是只能从训练数据集中找到一个最好的$f^*$，而这个$f^*$并不是真的$\hat{f}$，它只是$\hat{f}$的一个估计(estimator)。

就好比打靶，$\hat{f}$在靶心位置，而$f^*$则是几种靶子之后的一个位置。而$f^*$与$\hat{f}$总会有一些距离。这个距离有的来自于Bias，有的来自于Variance。

Estimator的Bias和Variance

我们现在来估计真实随机变量$x$。假设随机变量的均值(mean)是$\mu$，方差是$\sigma^2$。

而我们并不知道这个方差和均值等于多少，只能“估计”一下这个值。

Bias的估计

首先我们采样N个数据：${x^1, x^2, \cdots, x^N}$。对这N个数据我们估计它的均值是

$$m=\frac{1}{N}\sum_n x^n$$

但是，$m$只是$\mu$的一个估计，所以$m\neq\mu$。我们可以用这种采样的方法对$\mu$的值进行多次估计，所得到的$m$会在$\mu$附近震荡，如图。

用“期望”的方式表示，就是：

$$E[m]=E\left[\frac{1}{N}\sum_n x^n\right]=\frac{1}{N}\sum_n E\left[x^n\right]=\mu$$

重新梳理一下：我们首先通过对真实随机变量$x$进行采样，得到一系列样本。我们每次不同的采样，都会得到不同的样本。每次利用不同的样本，都会得到一个不同的“平均值”$m$。这个$m\neq\mu$，但是这个$m$的期望是等于$\mu$的。这就好比在打靶的时候，单次打靶的结果并不等于$\mu$，但随着打靶次数的增加，打靶的期望总会落在靶心上。而打靶的“分散程度”则是：

$$Var[m]=\frac{\sigma^2}{N}$$

这说明，当N比较多，$Var[m]$就会比较小。而当N比较少，$Var[m]$就比较大。

上图中上半部分就是N比较大的情况。这说明当我们采样的样本足够多的时候，得到的均值$m$能更好地接近$\mu$，而下半部分则是N比较小的时候。即当采样样本不足的时候，得到的均值$m$可能里$\mu$还比较远。

Variance的估计

同理，我们仍然采样N个数据：${x^1, x^2, \cdots, x^N}$。然后来估计它的$\sigma^2$：

首先计算均值

$$m=\frac{1}{N}\sum_x x^n$$

然后利用均值计算对$\sigma^2$的估计$s^2$：

$$s^2=\frac{1}{N}\sum_n(x^n-m)^2$$

与均值估计相同，我们需要了解这个$s^2$对$\sigma^2$的估计的优劣是多少。这里直接放结论：

$$E[s^2] = \frac{N - 1}{N}\sigma^2$$

即当N比较大的时候，分子分母之间相差的1几乎可以忽略。这个时候用$s^2$来表示$\sigma^2$是可以接受的。但当N比较小时，分子分母之间1的差距还是比较大的，这时候我们对$\sigma^2$往往会低估：

上图中从上到下三个轴表示N逐渐增大的情况。最上面N比较小的时候，我们会发现对$\sigma^2$的估计的$s^2$会比真实的$\sigma^2$小一些。但随着N的增大，这个估计会越来越大，并且逐渐倾向于等于$\sigma^2$。（具体原因参见统计学中关于有偏和无偏估计的部分）。

再回到Regression这个问题上。仍然以打靶举例。靶子代表整个函数空间（参数空间）。完美模型是$\hat{f}$，而我们每次打靶实际上是得到$f^*$。

如上图所示的靶子，靶心是真实模型$\hat{f}$，蓝色的小圆点为函数空间中的一个函数。棕色大圆点是多个函数的期望$\bar{f}$。以蓝色小圆点其中的一个点作为$f^*$为例子，从$\bar{f}$到$f^*$就是方差，表示每一个函数到这些函数中心点的散布程度。而从$\bar{f}$到$\hat{f}$的距离，则是这个估计模型到真正模型之间的偏差。

偏差就如同在打靶时，瞄准镜是歪的，每一枪都围绕着一个“有偏差”的目标附近。而围绕这个目标附近的散落程度则是方差。

如上图所示，Bias Variance的高低决定了四种不同的情况。最理想的情况是Low Bias和Low Variance（如左上）。说明打靶的瞄准很准，而且发挥也都很均匀。右上角说明尽管瞄准了，但每次打靶的水平发挥比较分散。左下角说明尽管发挥均匀，但瞄偏了，而右下角说明不但瞄准有偏差，而且水平方差也比较大。那么，这个结论对我们模型选择有什么意义呢?

模型的Bias和Variance

我们首先从方差的角度来看。

假设经过100次从真实分布中采样得到的训练数据，我们分别训练100个不同的模型。对于简单的模型（一阶）$y=b+w\cdot x$，它长这个样子：

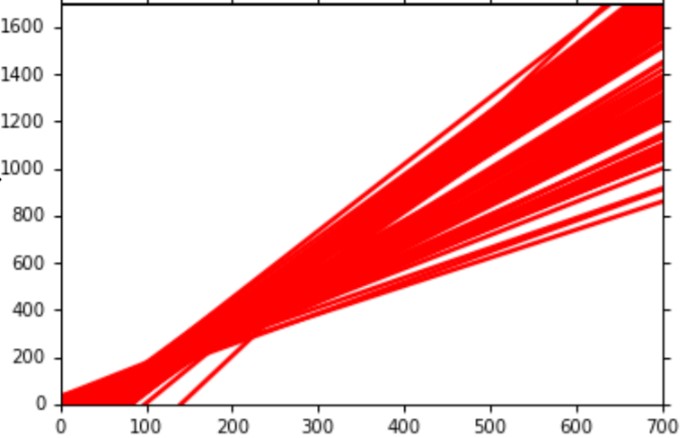
因为是一次模型，所以都是一堆直线组成。

而对于一个五阶的模型$y=b + w_1\cdot x + w_2\cdot x^2 + w_c\cdot x^3 + w_c\cdot x^4 + w_5\cdot x^5$，则是这样的：

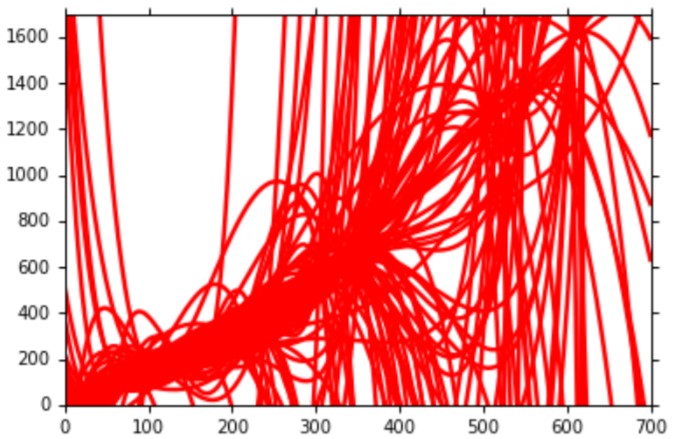
从图中我们能发现一个结论：越复杂的模型，variance就越大。因为简单的模型不容易受到数据本身噪声的影响。

然后从偏差的角度来看，假设我们的模型是一阶模型：

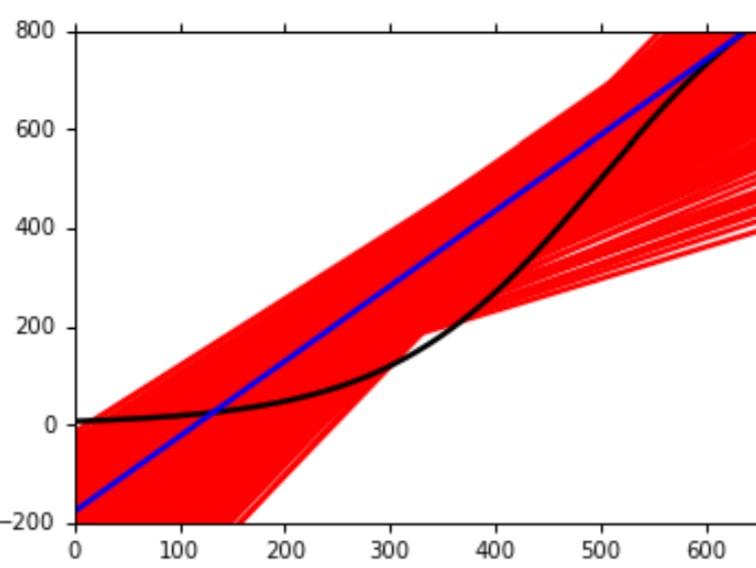
图中黑线是数据的真实分布。红色线是5000次实验得到的$f^*$，而蓝色线则是将这5000条曲线平均之后的结果。当用五阶模型时：

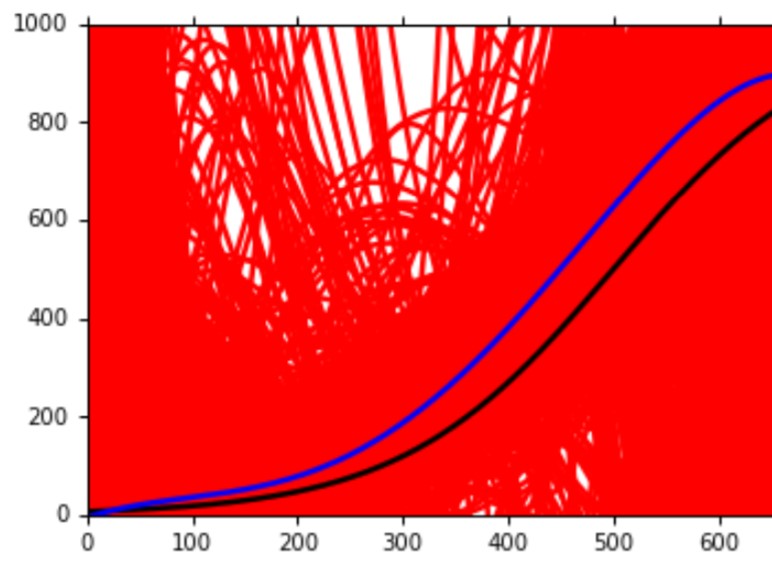
从图中能够发现，得到的蓝色的曲线距离黑色的真实分布近了一些。这说明一个结论：越复杂的模型，bias就越小。这说明因为模型复杂了，它包含的模型空间更大，所以它能够有更多的机会学习到正确的数据分布，尽管这个机会的方差比较大。

总结一下，就是这样的一张图：

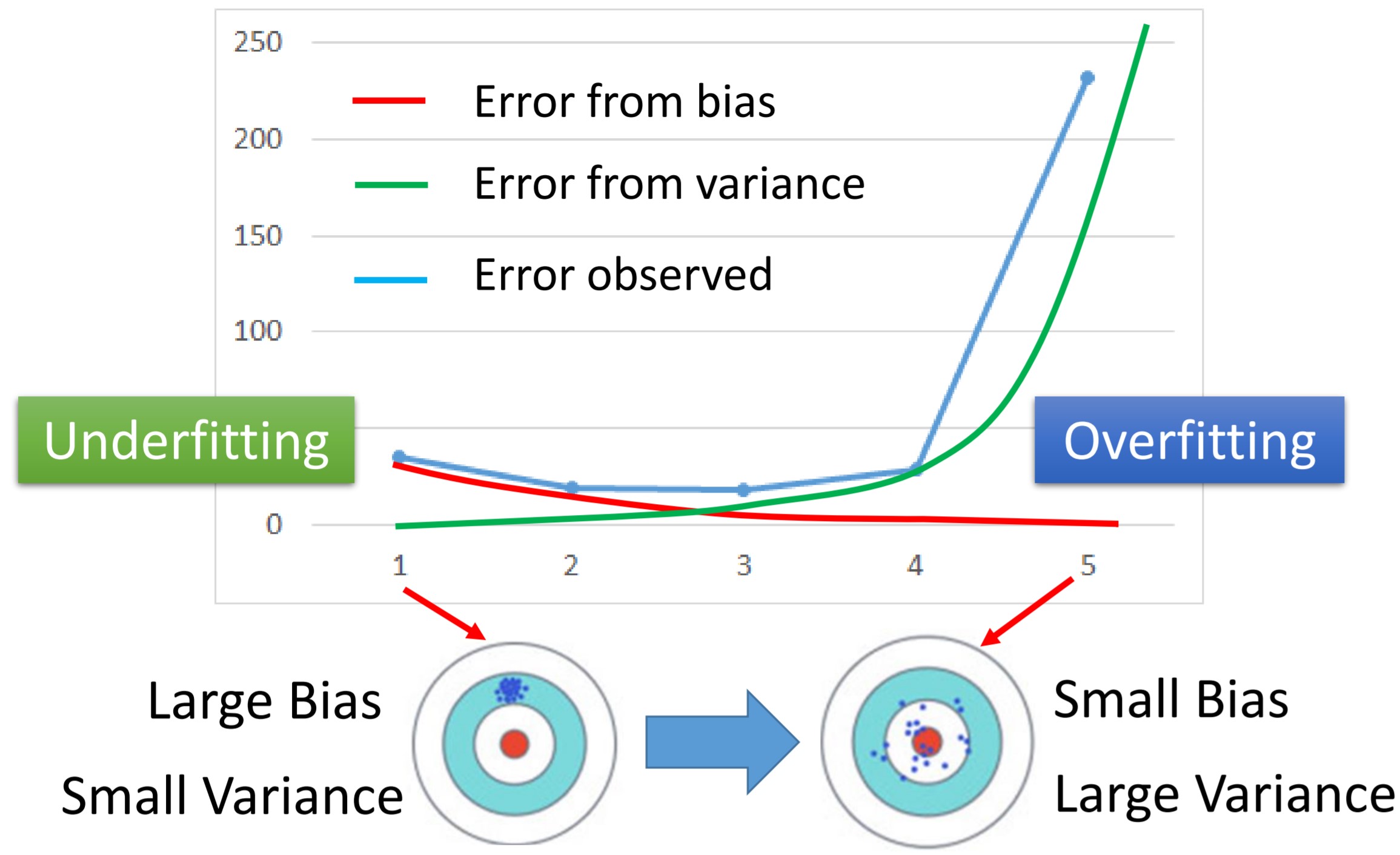
蓝色的线是我们在训练中观察到的误差曲线。模型的方差随着模型复杂程度增加而增加，而模型的偏差则由于模型更加复杂而减小。于是红色绿色两条线的交界点，则是理想的模型。

这些分析为我们在调试模型时提供了帮助：

1. 为了减小Bias
   • 增加更多的特征作为input：提升模型的阶数来增大模型的搜索空间。
   • 使用更复杂的模型：如果模型太简单，无论再怎么增加数据，都学习不到真实分布。
2. 为了减小Variance
   • 增加更多数据：增加数据是一个非常非常有效的方法。
   • 手工收集数据：但很多时候并不可行，成本很高。
   • 数据增强：通过自己对数据的理解，来变相地增加数据。 * 使用正则项：强行平滑模型

参考资料

1. 李宏毅深度学习视频：ML讲座1：回归 - 案例研究
2. 李宏毅深度学习视频：ML Lecture 2: Where does the error come from?